DONANIMDA ÇARPMA İŞLEMİ 1 : DADDA ALGORİTMASI
Toplama, çıkarma ve çarpma gibi temel aritmetik işlemler, dijital sistemlerin çekirdek yapı taşlarını oluşturur. Bu işlemler donanım üzerinde yüksek hızda gerçekleştirilebilir; ancak karmaşıklıkları ve kaynak maliyetleri birbirinden farklıdır. Bu temel işlemler arasında bölme, sıralı yapısı nedeniyle en karmaşık ve en fazla donanım kaynağı gerektiren operasyondur. Buna karşın çarpma işlemi, kısmi çarpımların paralel olarak oluşturulup toplanabilmesi sayesinde donanım düzeyinde daha verimli uygulanabilir. Bu nedenle, bir çarpma işlemini tek çevrimde (single-cycle) tamamlayabilmek donanım tasarımında önemli bir hedef olarak öne çıkar.
Çok çevrimli mimariler yerine tek çevrimde sonuç verebilen bir yapı, yüksek hız ve düşük gecikme sağlar. Fakat bu yaklaşım, paralel yolların artması nedeniyle alan tüketimini artırabilir. Bu noktada tasarımcı için amaç, performans ve donanım maliyeti arasında optimum dengeyi bulmaktır. Çarpma işlemi, bölmeye kıyasla optimizasyon açısından daha esnek bir yapıya sahiptir. Farklı mimari teknikler, örneğin dizisel (array) çarpanlar, kısmi çarpım azaltma ağaçları veya kodlama tabanlı yöntemler, sayesinde işlem süresi ve kaynak kullanımı dengelenebilir. Bu yazıda da, bu yaklaşımlar arasından yükseklik kontrollü azaltma prensibine dayanan bir yöntemi ele alacağız ve bu yöntemin donanımda tek çevrim çarpma hedefiyle nasıl kullanılabileceğini inceleyeceğiz.
Buraya kadar tam sayı (integer) çarpma işleminin donanımdaki önemini, tek çevrim hedefinin gerekliliğini ve farklı yaklaşımların genel farklarından bahsettik. Şimdi bu çarpma yöntemlerinden biri olan Dadda algoritmasını inceleyelim ve tam sayı çarpma işleminin donanımda nasıl tek çevrimde sonuç üretebildiğini adım adım görelim. Diğer çarpma algoritmalarına ise konunun devamı niteliğinde olacak başka bir yazıda daha kapsamlı biçimde değinebiliriz.

Yüksek hızlı çarpan tasarımlarında en kritik adım, Kısmi Çarpımların (partial products) verimli biçimde toplanmasıdır. Bu toplama işlemi sırasında kullanılan azaltma (reduction) stratejisi, çarpanın genel hızını doğrudan belirler. Dadda algoritması, bu azaltma sürecini olabilecek en az donanım kaynağıyla ve bu donanım kaynaklarıyla gerçekleştirilebilecek minimum gecikmeyle gerçekleştirmeyi hedefleyen, sütun yükseklik kontrolüne dayalı bir yöntemdir.
Dadda ağacı, kısmi çarpımları sütunlar hâlinde düzenler ve her sütunun yüksekliğini belirli aşamalarda sistematik olarak düşürür. Bu işlem, her aşamada Tam Toplayıcı (Full Adder) ve Yarım Toplayıcı (Half Adder) bloklarının kullanılmasıyla yapılır. Her sütundaki bit sayısı, bir sonraki aşamada belirlenen hedef yüksekliği (örneğin 6 → 4 → 3 → 2) geçmeyecek şekilde azaltılır.
Sonuçta elimizde, yalnızca iki satır hâline getirilmiş kısmi çarpımlar kalır ve bu iki satır donanımda hızlı bir toplayıcı (örneğin Carry Look-Ahead Adder) kullanılarak son çarpım sonucuna dönüştürülür.
Şimdi, bu yapının donanım düzeyinde nasıl gerçekleştirildiğine ve Dadda algoritmasının “tek çevrimde çarpma” hedefine nasıl ulaşabildiğine adım adım bakalım.
Dadda çarpma işleminin donanımda üç temel aşamadan oluştuğunu söylemiştik. Bunlar ;
- Kısmi çarpımların oluşturulması (Partial Product Generation)
- Kısmi çarpımların azaltılması (Partial Product Reduction)
- Sonucun elde edilmesi (Final Addition)
Dadda mimarisi bu süreci tamamen kombinasyonel bir yapı içinde, yani tek çevrimde tamamlayacak biçimde tasarlanır. Bu sayede, herhangi bir ardışık (sequential) kontrol yapısına gerek kalmadan, veriler girişten çıkışa tek bir mantık akışıyla ilerler.
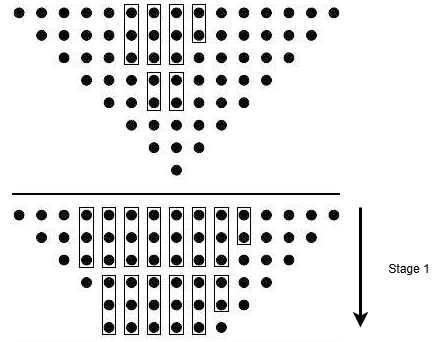
1-) Kısmi Çarpımların Oluşturulması (Partial Product Generation)
Dadda çarpma ağacının diyagramlarında görülen her nokta (•) aslında bir bitlik kısmi çarpımı (aᵢ·bⱼ) temsil eder. Örneğin 8×8 bitlik bir çarpma işlemi için toplam 64 adet kısmi çarpım üretilir. Bu bitler, aynı ağırlığa sahip olacak şekilde sütunlar hâlinde dizilir. Sütun indeksi (i+j), her kısmi çarpımın hangi ağırlığa ait olduğunu belirler. Böylece, en düşük sütun yalnızca bir bit içerirken, ortadaki sütun (örneğin ağırlık = 7) en fazla bite sahip olur.
Bu aşamada, girişteki her bit çiftini AND kapılarıyla çarparak kısmi çarpım matrisini oluşturabiliriz. HDL ortamında bu yapı iç içe generate döngüleri kullanılarak kolayca tanımlanabilir:
// ###################################
// ## 1. Partial Product Generation ##
// ###################################
genvar i, j;
generate
for (i = 0; i < 8; i = i + 1) begin : gen_rows
for (j = 0; j < 8; j = j + 1) begin : gen_cols
assign w_pp[i][j] = i_a_dadda8[j] & i_b_dadda8[i];
// Her bit çifti (a[i], b[j]) → 1 bit kısmi çarpım (•)
end
end
endgenerate2-) Kısmi Çarpımların Azaltılması (Partial Product Reduction)
Dadda algoritmasının kalbi, sütunlardaki yüksekliği sistematik olarak azaltmaktır. Bu azaltma işlemi sırasında aynı sütunda bulunan bitler 3’lü veya 2’li gruplar hâlinde işlenir. Bu noktada iki temel yapı taşından faydalanırız:
Full Adder (3:2 compressor) ve Half Adder (2:2 compressor).
3 nokta birleştirilmişse → Full Adder (3:2 compressor) kullanılır. Üç giriş biti → 2 çıkış üretir:
Sum = A ⊕ B ⊕ C
Carry = (A⋅B)+(B⋅C)+(A⋅C)
Burada “S” aynı sütunda kalırken, “C” bir sonraki sütuna taşınır.
2 nokta birleştirilmişse → Half Adder (2:2 compressor) devreye girer.
İki giriş biti → bir sum, bir carry çıkışı üretir.
// #################################
// ## 3:2 Compressor (Full Adder) ##
// #################################
module cla_dadda (
input i_A, i_B, i_Cin,
output o_Y, o_Cout
);
assign o_Y = i_A ^ i_B ^ i_Cin;
assign o_Cout = (i_A & i_B) | (i_A & i_Cin) | (i_B & i_Cin);
endmodule// #################################
// ## 2:2 Compressor (Half Adder) ##
// #################################
module HA (
input i_A, i_B,
output o_Sum, o_Cout
);
assign o_Sum = i_A ^ i_B;
assign o_Cout = i_A & i_B;
endmodule Bu yapılar, Dadda ağacındaki bit gruplarını sıkıştırmak için kullanılabilir. Örneğin aynı sütunda üç bit varsa fa_dadda, iki bit varsa ha_dadda kullanarak yüksekliği azaltırız. Bu adım sonunda, her sütun en fazla iki bite indirgenmiş olur.
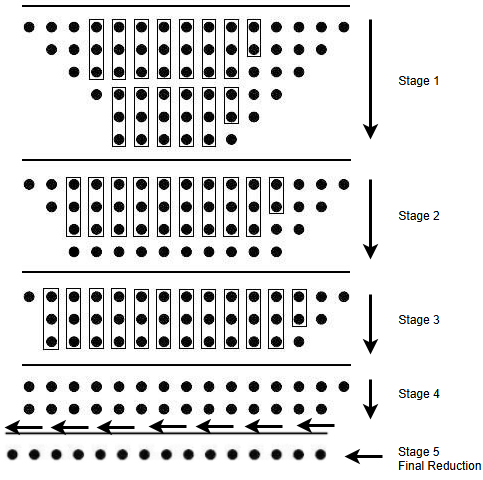
3-) Dadda Ağacının Katmanlı Yapısı (Final Addition)
Artık kısmi çarpımlar oluşturuldu ve azaltma işlemlerini tanımlayacak temel bloklarımız hazır. Sıradaki adım, bu iki bileşeni birleştirerek Dadda ağacının katmanlı yapısını kurmaktır. Her katmanda farklı yükseklik hedefleri belirlenir (örneğin 8→6, sonra 6→4, 4→3, 3→2). Bu aşamalar HDL tarafında, fa_dadda ve ha_dadda örneklerinin sistematik yerleşimiyle oluşturulur. Aşağıda bu yapının özetlenmiş bir hâli verilmiştir:
// ############################
// ## Dadda Multiplier (8x8) ##
// ############################
module dadda_8 (
input [7:0] i_a_dadda8, // Operand A
input [7:0] i_b_dadda8, // Operand B
output [15:0] o_ab_dadda8 // Result
);
// Partial Products
wire w_pp [0:7][7:0];
wire [0:5] r_s1, r_c1;
wire [0:13] r_s2, r_c2;
// Partial Product Generation
genvar i, j;
generate
for (i = 0; i < 8; i = i + 1)
for (j = 0; j < 8; j = j + 1)
assign w_pp[i][j] = i_a_dadda8[j] & i_b_dadda8[i];
endgenerate
// Stage 1: Reduction (8 → 6)
ha_dadda u_h1 (.i_A(w_pp[6][0]), .i_B(w_pp[5][1]), .o_Sum(r_s1[0]), .o_Carry(r_c1[0]));
fa_dadda u_f1 (.i_A(w_pp[7][0]), .i_B(w_pp[6][1]), .i_C(w_pp[5][2]), .o_Sum(r_s1[1]), .o_Carry(r_c1[1]));
// ... diğer stage’ler aynı prensiple devam eder
assign o_ab_dadda8[0] = w_pp[0][0];
assign o_ab_dadda8[15] = r_c2[13];
endmoduleBu yapıda her Stage, Dadda algoritmasının bir azaltma katmanını temsil eder. Katmanlar tamamlandığında elimizde sadece iki bitlik satırlar kalır; artık bu satırları toplama aşamasına geçebiliriz. Dadda ağacının tüm azaltma aşamaları tamamlandığında elimizde sadece iki satır kalır: biri Sum, diğeri Carry değerlerini taşır. Bu iki satır artık klasik bir toplayıcı devreyle (örneğin Ripple Carry Adder) birleştirilebilir. Bu aşamada işlemin tamamı hâlâ tek çevrimde (kombinasyonel) olarak gerçekleşir. Tasarımı nihai hale getirmek için tüm bu stageleri de modül içerisine ekleyerek tasarımımızı sonlandırabiliriz.
module dadda_8 (
input [7:0] i_A_dadda8,
input [7:0] i_B_dadda8,
output [15:0] o_AB_dadda8
);
// ############################
// ## Partial product matrix ##
// ############################
wire w_genPP [0:7][7:0];
// Stage wires
wire [0:5] w_S1, w_C1;
wire [0:13] w_S2, w_C2;
wire [0:9] w_S3, w_C3;
wire [0:11] w_S4, w_C4;
wire [0:13] w_S5, w_C5;
// ---------------------------------------------------------
// Generate Partial Products (AND Gates)
// ---------------------------------------------------------
genvar i, j;
generate
for (i = 0; i < 8; i = i + 1) begin : GEN_ROW
for (j = 0; j < 8; j = j + 1) begin : GEN_COL
assign w_genPP[i][j] = i_A_dadda8[j] & i_B_dadda8[i];
end
end
endgenerate
// #################################
// ## Stage 1 : Reduction (8 → 6) ##
// #################################
HA u_H1 (.i_A(w_genPP[6][0]), .i_B(w_genPP[5][1]), .o_Sum(w_S1[0]), .o_Cout(w_C1[0]));
HA u_H2 (.i_A(w_genPP[4][3]), .i_B(w_genPP[3][4]), .o_Sum(w_S1[2]), .o_Cout(w_C1[2]));
HA u_H3 (.i_A(w_genPP[4][4]), .i_B(w_genPP[3][5]), .o_Sum(w_S1[4]), .o_Cout(w_C1[4]));
cla_dadda u_FA11(.i_A(w_genPP[7][0]), .i_B(w_genPP[6][1]), .i_Cin(w_genPP[5][2]), .o_Y(w_S1[1]), .o_Cout(w_C1[1]));
cla_dadda u_FA12(.i_A(w_genPP[7][1]), .i_B(w_genPP[6][2]), .i_Cin(w_genPP[5][3]), .o_Y(w_S1[3]), .o_Cout(w_C1[3]));
cla_dadda u_FA13(.i_A(w_genPP[7][2]), .i_B(w_genPP[6][3]), .i_Cin(w_genPP[5][4]), .o_Y(w_S1[5]), .o_Cout(w_C1[5]));
// #################################
// ## Stage 2 : Reduction (6 → 4) ##
// #################################
HA u_H4 (.i_A(w_genPP[4][0]), .i_B(w_genPP[3][1]), .o_Sum(w_S2[0]), .o_Cout(w_C2[0]));
HA u_H5 (.i_A(w_genPP[2][3]), .i_B(w_genPP[1][4]), .o_Sum(w_S2[2]), .o_Cout(w_C2[2]));
cla_dadda u_FA21(.i_A(w_genPP[5][0]), .i_B(w_genPP[4][1]), .i_Cin(w_genPP[3][2]), .o_Y(w_S2[1]), .o_Cout(w_C2[1]));
cla_dadda u_FA22(.i_A(w_S1[0]), .i_B(w_genPP[4][2]), .i_Cin(w_genPP[3][3]), .o_Y(w_S2[3]), .o_Cout(w_C2[3]));
cla_dadda u_FA23(.i_A(w_genPP[2][4]), .i_B(w_genPP[1][5]), .i_Cin(w_genPP[0][6]), .o_Y(w_S2[4]), .o_Cout(w_C2[4]));
cla_dadda u_FA24(.i_A(w_S1[1]), .i_B(w_S1[2]), .i_Cin(w_C1[0]), .o_Y(w_S2[5]), .o_Cout(w_C2[5]));
cla_dadda u_FA25(.i_A(w_genPP[2][5]), .i_B(w_genPP[1][6]), .i_Cin(w_genPP[0][7]), .o_Y(w_S2[6]), .o_Cout(w_C2[6]));
cla_dadda u_FA26(.i_A(w_S1[3]), .i_B(w_S1[4]), .i_Cin(w_C1[1]), .o_Y(w_S2[7]), .o_Cout(w_C2[7]));
cla_dadda u_FA27(.i_A(w_C1[2]), .i_B(w_genPP[2][6]), .i_Cin(w_genPP[1][7]), .o_Y(w_S2[8]), .o_Cout(w_C2[8]));
cla_dadda u_FA28(.i_A(w_S1[5]), .i_B(w_C1[3]), .i_Cin(w_C1[4]), .o_Y(w_S2[9]), .o_Cout(w_C2[9]));
cla_dadda u_FA29(.i_A(w_genPP[4][5]), .i_B(w_genPP[3][6]), .i_Cin(w_genPP[2][7]), .o_Y(w_S2[10]),.o_Cout(w_C2[10]));
cla_dadda u_FA210(.i_A(w_genPP[7][3]),.i_B(w_C1[5]), .i_Cin(w_genPP[6][4]), .o_Y(w_S2[11]),.o_Cout(w_C2[11]));
cla_dadda u_FA211(.i_A(w_genPP[5][5]),.i_B(w_genPP[4][6]), .i_Cin(w_genPP[3][7]), .o_Y(w_S2[12]),.o_Cout(w_C2[12]));
cla_dadda u_FA212(.i_A(w_genPP[7][4]),.i_B(w_genPP[6][5]), .i_Cin(w_genPP[5][6]), .o_Y(w_S2[13]),.o_Cout(w_C2[13]));
// #################################
// ## Stage 3 : Reduction (4 → 3) ##
// #################################
HA u_H6 (.i_A(w_genPP[3][0]), .i_B(w_genPP[2][1]), .o_Sum(w_S3[0]), .o_Cout(w_C3[0]));
cla_dadda u_FA31(.i_A(w_S2[0]), .i_B(w_genPP[2][2]), .i_Cin(w_genPP[1][3]), .o_Y(w_S3[1]), .o_Cout(w_C3[1]));
cla_dadda u_FA32(.i_A(w_S2[1]), .i_B(w_S2[2]), .i_Cin(w_C2[0]), .o_Y(w_S3[2]), .o_Cout(w_C3[2]));
cla_dadda u_FA33(.i_A(w_C2[1]), .i_B(w_C2[2]), .i_Cin(w_S2[3]), .o_Y(w_S3[3]), .o_Cout(w_C3[3]));
cla_dadda u_FA34(.i_A(w_C2[3]), .i_B(w_C2[4]), .i_Cin(w_S2[5]), .o_Y(w_S3[4]), .o_Cout(w_C3[4]));
cla_dadda u_FA35(.i_A(w_C2[5]), .i_B(w_C2[6]), .i_Cin(w_S2[7]), .o_Y(w_S3[5]), .o_Cout(w_C3[5]));
cla_dadda u_FA36(.i_A(w_C2[7]), .i_B(w_C2[8]), .i_Cin(w_S2[9]), .o_Y(w_S3[6]), .o_Cout(w_C3[6]));
cla_dadda u_FA37(.i_A(w_C2[9]), .i_B(w_C2[10]), .i_Cin(w_S2[11]), .o_Y(w_S3[7]), .o_Cout(w_C3[7]));
cla_dadda u_FA38(.i_A(w_C2[11]), .i_B(w_C2[12]), .i_Cin(w_S2[13]), .o_Y(w_S3[8]), .o_Cout(w_C3[8]));
cla_dadda u_FA39(.i_A(w_genPP[7][5]), .i_B(w_genPP[6][6]), .i_Cin(w_genPP[5][7]), .o_Y(w_S3[9]), .o_Cout(w_C3[9]));
// #################################
// ## Stage 4 : Reduction (3 → 2) ##
// #################################
HA u_H7 (.i_A(w_genPP[2][0]), .i_B(w_genPP[1][1]), .o_Sum(w_S4[0]), .o_Cout(w_C4[0]));
cla_dadda u_FA41(.i_A(w_S3[0]), .i_B(w_genPP[1][2]), .i_Cin(w_genPP[0][3]), .o_Y(w_S4[1]), .o_Cout(w_C4[1]));
cla_dadda u_FA42(.i_A(w_C3[0]), .i_B(w_S3[1]), .i_Cin(w_genPP[0][4]), .o_Y(w_S4[2]), .o_Cout(w_C4[2]));
cla_dadda u_FA43(.i_A(w_C3[1]), .i_B(w_S3[2]), .i_Cin(w_genPP[0][5]), .o_Y(w_S4[3]), .o_Cout(w_C4[3]));
cla_dadda u_FA44(.i_A(w_C3[2]), .i_B(w_S3[3]), .i_Cin(w_S2[4]), .o_Y(w_S4[4]), .o_Cout(w_C4[4]));
cla_dadda u_FA45(.i_A(w_C3[3]), .i_B(w_S3[4]), .i_Cin(w_S2[6]), .o_Y(w_S4[5]), .o_Cout(w_C4[5]));
cla_dadda u_FA46(.i_A(w_C3[4]), .i_B(w_S3[5]), .i_Cin(w_S2[8]), .o_Y(w_S4[6]), .o_Cout(w_C4[6]));
cla_dadda u_FA47(.i_A(w_C3[5]), .i_B(w_S3[6]), .i_Cin(w_S2[10]), .o_Y(w_S4[7]), .o_Cout(w_C4[7]));
cla_dadda u_FA48(.i_A(w_C3[6]), .i_B(w_S3[7]), .i_Cin(w_S2[12]), .o_Y(w_S4[8]), .o_Cout(w_C4[8]));
cla_dadda u_FA49(.i_A(w_C3[7]), .i_B(w_S3[8]), .i_Cin(w_genPP[4][7]), .o_Y(w_S4[9]), .o_Cout(w_C4[9]));
cla_dadda u_FA410(.i_A(w_C3[8]), .i_B(w_S3[9]), .i_Cin(w_C2[13]), .o_Y(w_S4[10]),.o_Cout(w_C4[10]));
cla_dadda u_FA411(.i_A(w_C3[9]), .i_B(w_genPP[7][6]), .i_Cin(w_genPP[6][7]), .o_Y(w_S4[11]),.o_Cout(w_C4[11]));
// #######################################
// ## Stage 5 : Final Reduction (2 → 1) ##
// #######################################
HA u_H8 (.i_A(w_genPP[1][0]), .i_B(w_genPP[0][1]), .o_Sum(o_AB_dadda8[1]), .o_Cout(w_C5[0]));
cla_dadda u_FA51(.i_A(w_S4[0]), .i_B(w_genPP[0][2]), .i_Cin(w_C5[0]), .o_Y(o_AB_dadda8[2]), .o_Cout(w_C5[1]));
cla_dadda u_FA52(.i_A(w_C4[0]), .i_B(w_S4[1]), .i_Cin(w_C5[1]), .o_Y(o_AB_dadda8[3]), .o_Cout(w_C5[2]));
cla_dadda u_FA53(.i_A(w_C4[1]), .i_B(w_S4[2]), .i_Cin(w_C5[2]), .o_Y(o_AB_dadda8[4]), .o_Cout(w_C5[3]));
cla_dadda u_FA54(.i_A(w_C4[2]), .i_B(w_S4[3]), .i_Cin(w_C5[3]), .o_Y(o_AB_dadda8[5]), .o_Cout(w_C5[4]));
cla_dadda u_FA55(.i_A(w_C4[3]), .i_B(w_S4[4]), .i_Cin(w_C5[4]), .o_Y(o_AB_dadda8[6]), .o_Cout(w_C5[5]));
cla_dadda u_FA56(.i_A(w_C4[4]), .i_B(w_S4[5]), .i_Cin(w_C5[5]), .o_Y(o_AB_dadda8[7]), .o_Cout(w_C5[6]));
cla_dadda u_FA57(.i_A(w_C4[5]), .i_B(w_S4[6]), .i_Cin(w_C5[6]), .o_Y(o_AB_dadda8[8]), .o_Cout(w_C5[7]));
cla_dadda u_FA58(.i_A(w_C4[6]), .i_B(w_S4[7]), .i_Cin(w_C5[7]), .o_Y(o_AB_dadda8[9]), .o_Cout(w_C5[8]));
cla_dadda u_FA59(.i_A(w_C4[7]), .i_B(w_S4[8]), .i_Cin(w_C5[8]), .o_Y(o_AB_dadda8[10]), .o_Cout(w_C5[9]));
cla_dadda u_FA510(.i_A(w_C4[8]), .i_B(w_S4[9]), .i_Cin(w_C5[9]), .o_Y(o_AB_dadda8[11]), .o_Cout(w_C5[10]));
cla_dadda u_FA511(.i_A(w_C4[9]), .i_B(w_S4[10]), .i_Cin(w_C5[10]), .o_Y(o_AB_dadda8[12]), .o_Cout(w_C5[11]));
cla_dadda u_FA512(.i_A(w_C4[10]), .i_B(w_S4[11]), .i_Cin(w_C5[11]), .o_Y(o_AB_dadda8[13]), .o_Cout(w_C5[12]));
cla_dadda u_FA513(.i_A(w_C4[11]), .i_B(w_genPP[7][7]), .i_Cin(w_C5[12]), .o_Y(o_AB_dadda8[14]), .o_Cout(w_C5[13]));
// Direct Connections
assign o_AB_dadda8[0] = w_genPP[0][0];
assign o_AB_dadda8[15] = w_C5[13];
endmoduleBöylelikle tasarımı noktalamış oluruz.
